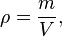29-Sep.14: The Relationship between Angular Speed and the Angle of a string

PURPOSE:
To derive a relationship between angular speed (ω) and the angle of the string above the vertical (θ) for a particular rotating apparatus.



The apparatus was a tall tripod, standing 211 centimeters high (h), with an attached motor which spun at a constant angular velocity.
At the top of the tripod was a rod, positioned perpendicular to the axis of rotation - we also attached a 165 centimeter string (L) to one end of the rod. At the bottom of the attached string, we tied a small mass. The radius of rotation (d) at the top of our apparatus was 61.5 centimeters.



 


We then measured, as a class, the amount of time it would take for 10 rotations to be completed.
After each measurement we took the average of the times.
After agreeing on a time, we measured the height (h2) of the hanging (now swinging at an angle) mass by slowly raising a piece of paper, which was attached to a sturdy pole, beneath the mass' swing-zone. We waited until the mass just barely tapped the paper, then quickly locked the paper-pole system into place and retrieved it for further measuring. We measured the height of the piece of paper (the very top of the paper where the mass came into contact with the paper) - this represents how high the swinging mass is above the ground.



We completed this process a total of eight times.
Below is a list of the times taken for 10 rotations paired with the height of the swinging mass for that run.

1) 37 sec. and 49 cm.
2) 30 sec. and 72 cm.
3) 26 sec. and 92 cm.
4) 25 sec. and 104.5 cm.
5) 23 sec. and 119 cm.
6) 21 sec. and 132 cm.
7) 19 sec. and 147 cm.
8) 17 sec. and 157 cm.

From the raw data, we recognized that with a smaller period (faster rotational velocity) there was an increased height of the mass.

We then found the period of each run by dividing the recorded times by ten (number of rotations).

T1) 3.7 sec.
T2) 3.0 sec.
T3) 2.6 sec.
T4) 2.5 sec.
T5) 2.3 sec.
T6) 2.1 sec.
T7) 1.9 sec.
T8) 1.7 sec.

Next, we calculated a value for theta (in radians) for each of the periods using the inverse cosine function.

Deriving a formula for the relationship between angular speed and the angle:

Using this derived expression we calculated values for omega for each of the experiments performed.

We then measured values for omega using the classic model,

Using our values for the first run, we found the values for the rest of the experiments using excel.

Using the ordered pairs (omega calculated, omega measured), we graphed our data to show how accurate our measurements were - a perfect measurement would cause a slope of 1 on the graph.

Our slope: 0.8740

A Great Day for Physics.

(taken:9/29/14 7:01am)

24-Sep.-14: Centripetal Acceleration as a function of Angular Speed

PURPOSE: To learn more about the modeling with Circular Motion by measuring the acceleration of a turn-table (with a radius of about 19 cm.) at various rotational velocities.

Our apparatus was a small, sturdy table which was free to rotate.
At one edge of the turn-table, we attached an accelerometer which collect the rotational velocity of the table.


 

As a class, we all collected the average period for different accelerations.
This was done with many stopwatches as we carefully timed how long it would take for the table to complete 3 rotations. We surveyed everyone's results after each measurement and averaged the times.

The times and accelerations:
1) t = 1.4 sec. and a = 32.8 m/s^2
2) t = 1.95 sec. and a = 16.4 m/s^2
3) t = 2.3 sec. and a = 12.9 m/s^2
4) t = 2.5 sec. and a = 12.1 m/s^2
5) t = 3.4 sec. and a = 6.0 m/s^2

After calculating values for each period and each rotational velocity, we then plotted our data on a centripetal acceleration-vs-rotational force graph, where the slope represents the radius of the circular motion. (a = r*w^2)

A great day for Physics.

(taken: 9/24/14 6:58am)

17-Sep.-14: Modeling Friction Forces

PURPOSE:
To learn more about measuring various frictional forces.

This lab included 5 parts (a through e), with all parts purposed to help us understand friction.


_________________________________________________________________________________
a) Static friction with cup and water

We began the first part by setting up our apparatus, which included a felt-bottom-block resting on the table surface tied to a string (I will reference this as end A).  Between both ends of the string was a pulley/wheel which was secured to the edge of the table. We let the string pass through the pulley and hang off the edge of the table - at this hanging end(end B), we tied a foam cup.


 

 



Our task for Part A was to measure the coefficient of static friction.

The process looked like this:

1. Weigh the mass of the block(s) tied to End A of the string.
2. Gradually fill the foam cup, at End B, with water until the block(s) resting on the table, begin moving. (Note: This point represents the value for the max. static friction)
3. Weigh the mass of the cup, with the water still in it.
4. Stack another block on top of the block which is tied to End A of the string.
5. Repeat all previous steps.

We repeated the experiment, adding one block to the system with each repeat until we had, at one point, four blocks stacked.

 Solving for the coefficient of the maximum static friction,

The values we calculated as a group were as follows:

We then plotted the data on a graph with a linear fit, however, before graphing we told the computer to graph without the fourth data point. We noticed during our calculations that something went wrong with the fourth piece, so we ignore it.

We made a plot of the Maximum Static friction force on the y-axis vs. Normal force on the x-axis.

This gave us the average coefficient for kinetic friction (slope) -  which turned out to be about 0.39.


_________________________________________________________________________________
b) kinetic friction with force sensor

For the second part, we needed to find the coefficient of kinetic friction.

Our apparatus for this part was simply a block (mass) tied to a force sensor, which we pulled at a constant velocity (roughly).

This allowed us to find the coefficient of friction using the force recorded on the force sensor, the mass of the block and using the known value of gravity.

Similar to part A, we measured four values (stacked multiple blocks).


 



To the best of our ability, we pulled a block at constant speed and got a measurement for the Tension force of each of the four measurements.









We then plotted the data from the four measurements on a Force-of-Pull-Vs.-Normal-Force graph.*
Analyzing this new graph, we found that the slope gave us the value for the coefficient of kinetic friction.

*Our graph went missing and our actual values for the forces were lost with the graph.

_________________________________________________________________________________
c) static friction from angle to get sliding

For the third apparatus we had an incline/ramp and a felt-bottom-block.
The plan was simply to increase the angle under the incline until the block began to move.
This value for theta would help us find the coefficient for static friction between the block and the ramp.

We measured an angle of 20 degrees for the incline just as the block began moving.



We found that the coefficient of static friction between the block and the ramp was 0.36, noting that for this particular set-up, the only information we needed was the angle of the ramp.


_________________________________________________________________________________
d) kinetic friction from sliding block on a steep ramp

For the fourth part of the activity, we used the same apparatus from part three. The difference in this new apparatus was an attached position sensor, at the top of the ramp.




 

Our goal for this part was to measure the coefficient for kinetic friction between the block and the ramp. We increased the angle of the incline to 30 degrees so that the block would accelerate down the incline, away from the sensor.
The acceleration of the block that we recorded through the sensor turned out to be 0.896m/s^2 and was in the direction parallel to the ramp.




The coefficient  for kinetic friction between the block and the ramp was calculated as 0.47.

_________________________________________________________________________________
e) predicting acceleration of a two-mass system—one on a friction ramp, the other hanging.

We performed the fifth part of the activity using the same apparatus as we did in part 4. The difference this time was that we moved the position sensor from the top of the ramp to the bottom - we also attached the pulley/wheel (from part 1) to the top of the ramp and hung a 500 gram mass, which was connected by a string to the 143 gram block on the ramp.





When we began part 5, we released the hanging mass from a reasonable height and collected the acceleration data through the sensor. The block was moving upward and parallel to the ramp.

Before we examined the sensor's value for the acceleration, we made a prediction for the acceleration using the known value for the coefficient of kinetic friction (0.47), the angle under the ramp(30 degrees), and the known values for each mass.

Our prediction for the acceleration of the block going up the ramp was calculated as 3.15 m/s^2.

We then plotted the sensor's collection data on a position-vs-time graph and a velocity-vs-time graph.
Specifically focused on the part of the graph with an increasing velocity, we were able to find an acceleration from the slope of the velocity-vs-time graph.

However, our graph (pictured above) may have contained some faulty data, or some unaccounted errors - we know this to be true because of the unreasonable value for slope (acceleration) which was 130.5 m/s^2.

A great day for Physics.

(9/15/14 7am)

8-Sep.-14: Propagated Uncertainty

PURPOSE: To learn more about error analysis and propagated uncertainty.

This activity was done in two parts. For the first part we measure the density of three different metals - for the second part, we determined an unknown mass.

Beginning the the equation of density, 

we suddenly realized what information was required to measure the density of our three metal cylinders. 

To measure the mass we used a provided mass scale which was accurate to 0.1 g.

To measure the diameter of each cylinder, we used calipers and divide the value to attain the radius.

The cylinders had a short enough height which allowed us to also use the calipers for that measurement.

The Data we collected:

Starting with the Volume of a cylinder,

we derived an expression to measure the uncertainty in the density of the cylinder given that we measure the mass, the diameter and the height of each said cylinder.

The value of density that we calculated for our Brass cylinder was 8,432 kg/m^3 ± 134kg/m^3.

_________________________________________________________________________________
_________________________________________________________________________________


For the Second part of the activity, we found the mass of an object using the concepts of tension and Newtons laws.

Our apparatus included two poles secured to a counter top with two strings supporting the unknown mass. Attached to one of the supporting strings was a spring scale to measure the tension in the string it is attached to.

Examining the apparatus of mass #6, we note that there is only one spring scale on the right string.

From the one scale we determined a value from the unknown mass.

A great day for physics.